Abstracts

• Mari Carmen Bañuls

  Tensor Networks: Entanglement and the Simulation of Quantum Many-Body Problems

  The term Tensor Network (TN) States designates a number of ansatzes that can efficiently represent certain states of quantum many-body systems. In particular, ground states and thermal equilibrium of local Hamiltonians, and, to some extent, real time evolution can be numerically studied with TN methods. Quantum information theory provides tools to understand why they are good ansatzes for physically relevant states, and some of the limitations connected to the simulation algorithms. 

  TNS were originally introduced in the context of condensed matter physics, where they have become a state-of-the-art technique for strongly correlated one-dimensional systems, but their applicability extends to many other fields. In particular, in the last years it has been shown that TNS are also suitable to study lattice gauge theories and other quantum field problems. This talk will give an overview of the possibilities and limitations of these methods, and some of their recent applications to this kind of systems.

• Arianna Borrelli

  Narrative Knowing and Approximations in High Energy Physics

  Scientific knowing is usually associated to logical-mathematical structures and is often used in narratology as an example of non-narrative communication. However, interdisciplinary research recently showed how narratives, too, can play a role in the construction of scientific knowledge both at the epistemic and at the socio-cultural level, which in practice can never be neatly separated from each other. These results do not stand in contrast to, but rather complement logical-mathematical analyses of science, allowing to grasp so far neglected aspects of past and present research cultures. I will discuss the role of narrative knowing in theoretical physics using as an example the first widely successful form of theories of everything: the Grand Unified Theories which emerged in the course of the 1970s.
  
  Since the late 1970s physicists have been searching for principles underlying all phenomena, from the nanophysical to the cosmic scale. Candidates for such a "theory of everything" appear to laypersons as coherent mathematical constructs, but in fact the mathematical elements of these theories are fragments bound together by words, diagrams and images which, together with the symbolic formulas, form a multi-medial construct telling a story, for example of how all different interactions are transformed when moving to higher and higher energy scales, to finally unify at the highest, experimentally unreachable energies.

• Nicolas Fillion

  The Logic and Semantics of Approximation in Models and their Solutions

  To a large extent, the history of applied mathematics is one of becoming increasingly more proficient at using inexact mathematics in scientific endeavors. It is thus no surprise that philosophers of science have become more concerned with idealization, approximation, and solutions obtained via perturbation theory or numerical methods. Yet, at the formal level, until a substantive account of the notion of approximate truth is developed, many of the general claims about the inferential and representational role of inexact mathematics remain “just so much mumbo-jumbo,” to use Laudan’s phrase. Of course, this claim is not meant to dismiss the undeniable value of informal or semi-formal accounts of the way in which approximate truth operates in scientific methodology. Rather, the point is that to make the sort of general claims that would be required to ground adaptations of the mapping account or the inferential account of representation in a way that incorporates the realities of inexact mathematics and the hard-earned wisdom developed by applied mathematicians, a more formal account of approximate truth would be needed. In the mapping and inferentialist accounts of representation, first-order logic and its underlying satisfaction semantics remain the guiding paradigm. This being the case, based on the formal work of applied mathematicians in perturbation theory and numerical analysis, this talk systematically examines the analogies and disanalogies between truth semantics and approximate truth semantics, thereby showing that the two styles of semantics have radically different modi operandi.
  
  Section 1 of the paper highlights the semantic distinction between classificatory and quantitative concepts, in the spirit of the measurement theory pioneered by Scott & Suppes. Section 2 argues that the notion of satisfaction and validity relevant to inexact representation cannot be treated using the standard syntactic (schematic) tools of formal logic, a key point for handling quantitative concepts. Section 3 abstracts the main operational concepts used to semantically assess inexact representation and inferences from the methods deployed in perturbation theory and numerical methods. Finally, section 4 isolates the conditioning of model equations as a hybrid concept combining the relevant internalist and externalist features that effectively enables scientists to correctly assess their inexact representations and inferences.

• James Fraser and Alexander Blum

  Rigorous Approximation: The Origins of the Causal Perturbation Theory Programme

  The 1950s saw a new phase of mathematically-orientated work on the foundations of quantum field theory (QFT). The most well-known programme to emerge from this period was the axiomatic approach to QFT, which attempted to move beyond the conventional perturbative treatment of the theory and write down sets of principles which could be expected to hold outside of perturbation theory. This paper unearths the second strand of mathematical work on QFT which focused on shoring up the foundational standing of the perturbative approximation scheme itself. We examine the work of Ernst Stueckelberg, Nicolay Bogoluibov and their collaborators in the 1950s which laid the groundwork for what is now a days called the causal perturbation theory approach. This programme has important implications for how we understand the perturbative renormalization procedure and the problem of ultraviolet divergences. Here, however, we focus on broader lessons, as the causal perturbation theory programme arguably complicates sharp distinctions between reconstructive projects in mathematical physics and the messy, unrigorous, approximation techniques employed in the physics mainstream.

• Josh Hunt

  Reformulations in Perturbative QFT

  The empirical success of particle physics rests largely on an approximation method: perturbation theory. Yet even within perturbative quantum field theory, there are a variety of different formulations. I will compare and contrast two compatible formulations of perturbative QFT: (i) traditional Feynman diagram methods and (ii) a recent method known as on-shell recursion. Due to how quickly the number of terms grows in perturbation theory, Feynman diagrams become infeasible for calculations involving many particles. Within the past 15 years, physicists have reformulated perturbation theory using spinor--helicity variables and complex analysis, leading to more tractable recursion relations for computing amplitudes. This case study shows how reformulating an approximation method can be a source of tremendous progress in physics---a source very different from constructing new theories.
  
  Much of this progress comes from changing the variables used to describe scattering amplitudes. Different choices of variables make certain properties or patterns manifest. For instance, an incredibly simple relationship known as the Parke--Taylor formula requires hundreds of pages to prove using Feynman diagrams but only a three-page inductive proof using the on-shell formulation. Progress in particle physics often comes from figuring out how to re-package perturbation series into ever more convenient forms, where otherwise-mysterious cancellations become clear. In addition to considering the practical and epistemic dimensions of reformulating, I will illustrate my account of the epistemic value of making properties manifest.

• Michael Miller

  On the Common Structure of Perturbative and Axiomatic Field Theory in Borel Summable Models

  Interpreters of perturbative and axiomatic field theory have typically been thought to face distinct sets of obstacles. Perturbative field theory, while empirically successful, employ approximation schemes that stand in tension with standard approaches to theory interpretation. Axiomatic field theory, while admitting to exact models, does not enjoy the same empirical success. Or at least, so the standard story goes. In this talk, I problematize this understanding of the situation by considering a collection of results that establish that perturbative and axiomatic field theory share a common structure for a restricted class of models. This analysis establishes a precise sense in which the central interpretative problems facing the perturbative and axiomatic frameworks are actually one and the same. I conclude by articulating one approach to facing up this interpretative problem.

• Michiyo Nakane

  The Role of Approximation Thought in the Development of the Hamilton-Jacobi Theory

  This talk surveys the development of the Hamilton-Jacobi theory, particularly its derivation from Hamilton and Jacobi’s ideas of approximation.

  In 1833, W. R. Hamilton developed what was called Hamilton’s function when he tentatively applied his characteristic function, which he had developed in a study of geometrical optics, to the three-body problem formed by the Sun, Jupiter, and Saturn.  In 1836, C. G. J. Jacobi encountered a force function explicitly involving a time when he discussed another three-body problem involving the Sun, Jupiter, and a comet. Then he got the idea of expanding Hamilton’s results from conservative systems to non-conservative ones, so the force function explicitly involved time.

  Although mathematically interesting, their main theorem of reducing the solution of dynamical equations to that of a partial differential equation was practically effective in very limited cases, such as the Keplerian problem. However, when bound with canonical perturbation theory, which was originated from Jacobi and developed by his successors in the late 19th century, their main theorem, at last, became useful in practice. This talk also examines this process more precisely noting the introduction of the action-angle variables.

• Sébastien Rivat

  Steve Weinberg and the Rise of Systematic Low-Energy Approximations

  Bottom-up effective field theories (EFTs) have taken an increasingly central place in physics practice since the early 1980s, opening, in particular, new ways of capturing systematically the effects of high-energy physics at low energies. Despite this growing importance, their historical development remains largely uncharted so far. In this talk, I trace the origin of bottom-up EFTs, identifying some of their most significant historical roots in Steven Weinberg’s works in the 1960s. Although his approximation scheme is rudimentary at this stage, we can still identify (or so I will argue) key defining features of bottom-up EFTs in these early works. I will also show that Weinberg’s first prototype of effective theory was decisively shaped both by his appeal to soft particle approximation methods and by his broader unificatory aspirations.

• Pablo Ruiz de Olano

  Too Strong for Perturbation Theory? Physicists’ Attempts to Measure the Value of the Pion-Nucleon Coupling Constant, and a Difficulty about the Confir

  Histories of high-energy physics often tell us that, although physicists tried to apply perturbation theory to the Yukawa theory during the 1940s and 1950s, their efforts ultimately failed. Such claims are often coupled, in fact, with an additional remark accounting for the reasons behind their lack of success: the numeric value of the coupling constant in Yukawa’s theory is greater than one, and the theory is therefore not amenable to a perturbative treatment. In this paper, I examine physicists’ actual attempts to determine the value of this constant, as they unfolded during the 1940s. As I show, this process was much more intricate than standard histories of high-energy physics would have us believe, and it in fact points to an important difficulty in the confirmation of quantum field-theoretic models.

  My story begins in the early 1940s, with the attempts made by Heisenberg, Bhabha, and Heitler to apply perturbation theory to the then newly formulated Yukawa theory. It then continues with the so-called strong coupling approach that Wentzel, Serber, and others developed during the next few years, and it culminates with Kenneth Case’s efforts to apply Dysonian renormalization theory to this same problem. As we shall see, various conclusions were drawn about the value of the coupling constant in the Yukawa theory from the repeated failures of all three of these approaches, the idea that the coupling constant was greater than one, and the strong force too strong for perturbation theory, being a recurring theme during this period.

  I then go on how some of the historical actors in the case study realized this conclusion to be mistaken. Physicists’ efforts to extract empirical predictions out of the Yukawa theory, after all, were invariably mediated by the use of an approximation method, and they always made use of the basic framework provided by quantum field theory. When physicists’ predictions failed to match experimental data, therefore, there was no way of knowing if blame was to be placed on the Yukawa theory itself, on the approximation method attached to it, or on the formalism of quantum field theory as a whole. I conclude by arguing that this analysis applies to the confirmation of quantum field-theoretic models in general and that it casts some doubt on current approaches to fundamental physics, which privilege model building at the expense of approximation methods.

• Jens Salomon and Alexander Blum

  Nothing Comes from Nothing but the Rho Meson - the Origin of the Bootstrap Notion in Particle Physics

  While establishing a novel framework for the study of the pion-pion interaction together with Stanley Mandelstam, Geoffrey Chew referred to one of its solutions as the "'bootstrap' mechanism" in a talk in 1959. By using this metaphor, he introduced a notion into particle physics that was about to gain lots of currency. However, while its metaphorical origin kept the bootstrap notion malleable such that it could outlive 
  shifts in underlying research programs, its metaphorical origin might also explain why it is considered hard to give a clear-cut definition of the bootstrap notion. This situation is exacerbated by the fact that Chew and Mandelstam mention, but do not elaborate on the bootstrap notion in their pertinent publications - presumably because of Mandelstam's reluctance to endorse the notion. Nevertheless, in this talk we tackle the quest of defining the bootstrap notion - at least at its origin.

  The purpose of this talk is to propound a compelling interpretation of the bootstrap notion as it was first used by Chew. As will be elaborated, Chew and Mandelstam established a framework that allowed for the investigation of the pion-pion interaction. This framework 
  permits quantitative predictions although it was founded on general principles such as Lorentz invariance, causality, unitarity, and crossing symmetry only. Particularly, the framework did not require the specification of the pion-pion interaction by a Lagrangian. The framework contains only one free parameter. Basically, in the framework, the interaction strength of pions in a certain scattering channel is driven by the free parameter plus by the interaction of pions in crossed scattering channels. Strikingly, there is one non-vanishing solution of the framework that does not depend on the free parameter. For this solution, the pion-pion interaction sustains itself (through crossed channels) even if the value of the free parameter vanishes - the solution "bootstraps" itself. Even more strikingly, the character of this non-vanishing solution is in qualitative accordance with the 
  properties of the rho meson, whose discovery was in progress in those days.

  Based on a reconstruction of Chew and Mandelstam's argumentation, their usage of approximations will be expounded. It will be argued that while their framework does not prompt the bootstrap interpretation, only the application of approximations to it lays the groundwork for its conception. Chew and Mandelstam's course of action hence exemplifies 
  that approximations can advance physics in their own unique way.

• George Smith

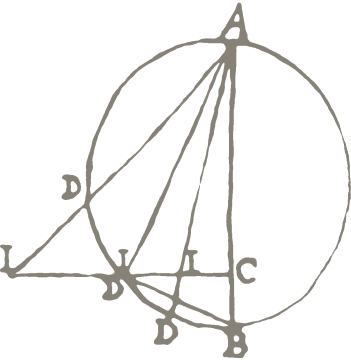
  Approximation in Newton’s Principia

  From the very beginning of his efforts toward the Principia, Newton had concluded that any representation of orbital motions in our planetary system can only be an approximation to the actual motions of the bodies among themselves – not just because of the limits of precision of observations, but far more so because the interactions among the bodies make the actual motions too complicated ever to admit to exact representation. Much of the Principia can be read as endeavoring to show that one particular approach to approximating the motions, namely as arising from inverse-square gravitational forces directed toward the bodies in the system, is to be preferred on physical grounds to other comparably accurate approximations. To this end, Newton first requires all inferences from approximate representations of the motions to hold to at least the same level of approximation. He then pursues the goal of showing that every systematic discrepancy between observation, on the one hand, and those representations and inferences, on the other, results from a robust physical source, thereby providing evidence that the inferences are physically well-founded, and the representations of the motions, approximate though they are, are as well.

• Monica Solomon

  Approximations with or without a Method

  There is no denying that the practice of physics involves a patchwork of conceptual techniques and methods (Wilson 2008). As Batterman (2001) shows, paradigmatic examples involve methods in which universality is achieved by means of “eliminating irrelevant details about individual systems.” Along this line of research, recent scholarship emphasized the significance of approximation methods on their own, understood separately from models or idealizations (Norton 2012). For example, Ruiz de Olano et al (2022) explain that important cases of approximation methods have a distinct category of theoretical results than idealization. Moreover, the models invoked in idealizations rely on approximations to get their empirical content in the first place. Yet, philosophers of science have focused so far on the methods involved in limits of infinite systems (from statistical mechanics or quantum theory). This paper takes a different focus on approximations: I investigate the historical case of Newton’s original researches in dynamics. Newton’s case is interesting because there seem to be several kinds of approximations developed in his Principia (and the research leading up to it). First, I survey three examples of approximations. (1) The kinds of approximations involved in approximations of orbital motion, (2) approximations needed for the Kepler problem (Book 1, Prop 31), and finally (3) the approximation of the air drag (”retardation”) in the experiment of double pendulum collisions described in the scholium to the laws of motion. Second, my analysis of these cases is limited to revealing the kinds of choices involved in the crafting of the approximation. I am also interested in investigating whether there are different kinds of approximations. Finally, I raise and approach the questions driving this comparison: (a) is there a principled method behind these approximations? and (b) what are the constraints which operate in each case?