Optical dispersion is the phenomenon we observe in rainbows and in the spectra produced by prisms. Although easy to observe, optical dispersion has been a very difficult phenomenon to model ever since Newton’s first attempts, being at the border between theories of light and matter.
Between the end of the nineteenth and the beginning of the twentieth century, the various interpretations of optical dispersion played a central role in two very different revolutions: the emergence of microphysics around 1900, and the birth of quantum mechanics in 1925. The purpose of this research, as part of the project on “History and Foundations of Quantum Physics” of Department I, is to reveal the features that made optical dispersion a persisting problem during this period, and thus to clarify how quantum physics developed from classical physics.
From the 1870s onwards, all theories of optical dispersion made use of the same fundamental model of light-matter interaction: the Mitschwingungen, translatable as covibrations. This model provided physicists with a powerful and fruitful conceptual tool to describe the interaction between light and matter, from classical to quantum theories. More importantly, it was embedded over time into different conceptual frameworks and ontologies, while maintaining the same basic structure. Focusing on the long-term history of optical dispersion, this research aims at understanding how, through this combination of flexibility and stability, the model of Mitschwingungen transmitted the knowledge on light and matter across the quantum divide.
Before the introduction of Mitschwingungen, it was commonplace to conceive of light as a periodical perturbation of an invisible substance that filled everything: the ether. There was no attempt to take the motion of particles of matter into account to explain optical phenomena. Furthermore, the spectrum of dispersed light was hitherto believed to present an invariable succession of colors in the order violet, blue, green, yellow, orange and red.
However, in 1871-1872, a surprising feature, ranked by Thomas Preston (1860-1900) in 1890 “among the most singular of the discoveries of modern times,” caused the above-mentioned presumptions to change: Christian Christiansen (1843-1917) and August Kundt (1839-1894) independently observed that under certain circumstances the spectrum seemed to invert, to “return upon itself.” Since then, in order to explain both the “normal” and these “anomalous” patterns of optical dispersion, it became necessary to include assumptions about the molecular behavior in optics. It was in this spirit that Wolfgang Sellmeier developed the new conceptual tool that would lay down the foundations for any other theoretical picture of light-matter interaction until quantum mechanics: the Mitschwingungen. The idea boiled down to the hypothesis that dispersion stemmed from an interaction between light waves and particles of matter vibrating at specific frequencies, which were the resonance frequencies of the system.
Precisely because of its dual nature optical dispersion quickly became a hot topic in optics, together with Mitschwingungen as an indispensable conceptual tool. After Sellmeier, many prominent German theorists approached the issue of optical dispersion by applying this model; among others, Hermann von Helmholtz (1821-1894), Woldemar Voigt (1850-1919), Paul Drude (1863-1906), and Eduard Ketteler (1836-1900).
In the last decade of the century, the Mitschwingungen model was embedded into a new physical theory that was spreading in Germany: electromagnetism. Electromagnetism provided an effective way of unifying optical, electric and magnetic phenomena. In this new context, Mitschwingungen could be easily reinterpreted as an interaction between vibrating charged particles and electromagnetic light, while its basic mathematical structure remained unchanged. In 1897 the discovery of the smallest charge of electricity, the so-called “electron,” introduced another important aspect. Indeed, the experimental determination of the microphysical properties of the electron led Hendrik Antoon Lorentz (1853-1928) and Drude to link the above-mentioned view of Mitschwingungen to specific features of the structure of matter. More precisely, by combining experimental data on the electron with the theoretical model of Mitschwingungen it became possible to relate optical dispersion with physical and chemical properties of matter, notably the valence. In this way, optical phenomena could be used as a tool to explore the microstructure of matter. Alongside the theoretical insights, also the development of more reliable experimental setups was essential for the microphysical turn of optics. In particular, the extreme precision that optical dispersion measurements required called for novel experimental methods combining interferometers and refractometers.
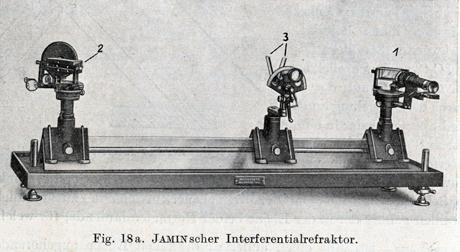
Fig. 2: Experimental setup to measure optical dispersion with extreme precision, combining an interferometer with a refractometer. In: M.v.Laue (1928), “Interferenz und Beugung elektromagnetischer Wellen”, 211-365, in Handbuch der Experimentalphysik, Band 8, Akademische Verlagsgesellschaft M.B.H., Leipzig
It was against the background of such intimate connection with specific features of the microstructure of matter that in 1913 the Mitschwingungen model came into conflict with another new theory of physics: the quantum theory. That year, the young theoretical physicist Niels Bohr (1885-1962) proposed the first quantum model of matter, which was immediately and generally accepted by the physics community. According to this model an electron moved around the atomic nucleus along “quantum orbits” and the absorption or emission of light corresponded to a discrete jump of the electron to a higher or lower orbit respectively. This model was apparently irreconcilable with Mitschwingungen because of two reasons. Firstly, Mitschwingungen called for a model of matter in which electrons exchanged energy with light continuously, contrary to Bohr’s model. Secondly, Mitschwingungen required the color of the emitted or absorbed light to be univocally determined by the mechanical vibration of the electron in the atom, while in Bohr’s model the color of light depended on the electron jump and not on the mechanical orbit.

Fig. 3: Arnold Sommerfeld in Zürich 1926 mit Annie Schrödinger und Peter Debye. Source: Sommerfeld-Projekt, Lehrstuhl für Geschichte der Naturwissenschaften, Ludwig-Maximilians-Universität München.
Mitschwingungen, however, was still the most satisfactory model to describe the experimental data on optical dispersion. Hence, in the ensuing years, it became necessary to find a way to solve the conflict between this model and Bohr’s. This process led to two different outcomes, both modeling optical dispersion as Mitschwingungen but attributing different physical nature to the oscillating entities that interacted with electromagnetic light. On the one hand, Arnold Sommerfeld (1868-1851) and Peter Debye (1884-1966) tried to conciliate the two alternatives. They developed a picture in which the model of classical Mitschwingungen was applied directly to Bohr’s orbits, that is to say, in their theory the electromagnetic light interacted with “vibrating orbits,” instead of vibrating electrons. This theory worked very well for a few types of simple molecules, but it was very difficult to extend to molecules with complicated structure.
On the other hand, Rudolf Ladenburg (1882-1952) in the early 1920s put forward a radical reinterpretation of the model. Exploiting the potential of the model of Mitschwingungen as an analogy within the quantum formalism, Ladenburg pictured the light-matter interaction in terms of a new concept, “Ersatzoscillatoren,” later called “virtual oscillators.” The peculiarity of these oscillators was that they did not correspond to any physical entity, such as electrons or orbits, but to the Bohrian jumps themselves. Ladenburg’s model altogether relinquished any description of electronic paths, and the new concept of “virtual oscillators” triggered a shift of focus in the entire quantum theory: Bohrian quantum jumps took the place of mechanical orbits. This rearrangement laid out the conceptual grounds for quantum mechanics. In 1925, Werner Heisenberg (1901-1976), the father of matrix mechanics and one of the towering figures of the quantum revolution, called optical dispersion one of “the most important steps toward quantum-theoretical mechanics.”
Thus after being transmitted across two revolutions and adapted to the most contrasting conceptual frameworks (ether theory, electromagnetic theory, quantum theory) Mitschwingungen finally became one of the pillars of new quantum mechanics. On the one hand, this model yielded a basic and easily conceivable structure that led to satisfactory results. On the other hand, it was flexible enough that its constitutive elements (waves and oscillators) could be translated into different physical languages. In fact, it was the persistence of the model over different ontologies that predisposed it to being introduced as a “virtual” analogy in quantum physics. The story of optical dispersion shows how deeply quantum physics is rooted in classical physics.